Home » Misc » Определение жесткости

Определение жесткости


Описание методов определения жесткости воды

Описание метода комплексонометрического титрования с ЭДТА и колориметрического метода с кальмагитом.

 

  • Определение жесткости воды титрованием.
  • Определение жесткости воды колориметрическим методом
  • Описание химических реакций при определении общей и кальциевой жесткости воды методом титриметрического и колориметрического анализа.

Жесткость воды вызвана растворенными в ней минералами, в первую очередь двухвалентными катионами, включая кальций (Ca2+), железо (Fe2+), стронций (Sr2+), цинк (Zn2+) и марганец (Mn2+). Ионы кальция и магния обычно являются единственными ионами, присутствующими в значительных концентрациях; поэтому считается, что жесткость является мерой содержания кальция и магния в воде. Тем не менее следует учитывать случаи, когда другие катионы, влияющие на жесткость, присутствуют в значительных количествах.

 

Определение жесткости воды титрованием

Жесткость воды можно быстро определить титриметрическим методом с использованием индикаторов. При правильном выборе водородного показателя pH можно измерить общую жесткость (Ca2+ и Mg2+) или долю кальция и магния по отдельности. Традиционный тест на жесткость включает доведение уровня pH до 10,1 аммиачным буфером, добавление индикатора эриохрома черного Т [1- (1-гидрокси-2-нафтилазо) -6-нитро-2-нафтол-4-сульфоновую кислоты] и титрование раствором Na2 ЭДТА (динатриевая соль этилендиаминтетрауксусной кислоты).

Некоторые индикаторы более стабильны, дают более быструю реакцию и более четкую конечную точку, чем эриохром черный T. Одним из лучших является кальмагит, 1- (1-гидроксил-4-метил-2-фенилазо) -2-нафтол-4 сульфоновая кислота, который используется в тест наборах и реагентах Hach Lange для определения общей жесткости воды.

 

Определение жесткости воды колориметрическим методом

Колориметрический метод измерения жесткости дополняет традиционный титриметрический метод, поскольку колориметрический метод позволяет измерять очень низкие уровни кальция и магния (0,05 - 4,00 мг/л Ca и Mg в виде CaCO3). Взаимодействие некоторых металлов с методами титрования после разбавления пробы станет несущественным, попадая в диапазон этого теста. В тесте используются индикатор кальмагита и два хелатирующих агента, EGTA (этиленгликоль-бис (β-аминоэтиловый эфир) -N, N, N ', N'-тетрауксусная кислота) и ЭДТА.

 

Описание химических реакций

Определение общей жесткости

Далее будут описаны некоторые растворы и картриджи производителя Hach Lange для титрования подготовленных проб воды в которых содержится индикатор кальмагит. Титрант для определения жесткости TitraVer (0,020 н. ЭДТА) является наиболее широко используемым. В ассортименте представлены другие концентрации титранта TitraVer предназначенных для образцов с высоким уровнем жесткости. Также доступен титрант HexaVer - это ЦГДТА (циклогексан-транс-1,2-диамин тетрауксусная кислота). Он дает более четкие конечные точки и может выдерживать более высокие уровни помех от железа, чем TitraVer.

Индикатор кальмагит доступен в специальных составах ManVer и UniVer. Составы с кальмагитом ManVer специально приготовлены для повышения стабильности и отсутствия помех от большинства элементов в пробе. Помехи, вызванные ионами металлов, таких как медь или железо, можно удалить или замаскировать с помощью магниевой соли ЦГДТА, что эффективно и в то же время безопасно при использовании. Для удаления интерференций также могут использоваться соединения с содержанием цианидов. По возможности следует избегать их использования ввиду потенциальной опасности для окружающей среды и здоровья. 

Реакция кальмагита зависит от pH; определено, что pH 10,1 является идеальным. Традиционно использовались аммиачные буферы; однако у них сильный специфический запах. В методах Hach используется буфер Hardness 1 (2-амино-2-метил-1-пропанол), который стабилен, безопасен в использовании c менее неприятным запахом.

Последовательность анализа в тестах на жесткость начинается с регулирования pH и добавления ингибиторов с последующим образованием комплексов Mg2+ и Ca2+ с кальмагитом. При этом значении pH кальций образует слабый комплекс с кальмагитом. Раствор титруют TitraVer (ЭДТА) или HexaVer (ЦГДТА). Титрант сначала связывает любой кальций, затем магний. Изменение цвета от винно-красного до синего свидетельствует о том, что весь кальций и магний были удалены из кальмагита и образовали комплекс с титрантом.

Выражение результатов титрования жесткости - мг/л CaCO3. Реакция TitraVer с Ca2 + и Mg2 + является соотношением 1:1.

Определение кальциевой жесткости

Тест на кальциевую жесткость пробы воды очень схож с тестом на общую жесткость. Обычно после индикатора мурексида (пурпурат аммония) или индикатора эриохром сине-черный R следует титрование с ЭДТА. Индикатор CalVer 2 разработан компанией Hach для замены этих индикаторов. CalVer 2 (гидроксинафтол голубой) более чувствителен с более резким изменением цвета конечной точки.

Индикатор CalVer 2 образует красно-фиолетовый комплекс с кальцием и меняет цвет на синий после того, как TitraVer удаляет кальций из комплекса. Уровень pH повышается по крайней мере до 13 для осаждения магния. К реакционной смеси можно добавить несколько капель стандартного раствора магния, чтобы усилить изменение цвета конечной точки. Это может показаться противоречивым, так как магний осаждается при повышении pH. Однако, добавленный магний предпочтительно хелатируется красителем, и его количество очень мало; таким образом, любая погрешность, вызванная добавлением магния, незначительна.

Регулировка pH осуществляется добавлением гидроксида калия перед добавлением CalVer 2. Для связывания металлов вызывающих помехи можно добавить цианид калия перед добавлением CalVer 2.

Кальциевую и общую жесткость можно определять последовательно с использованием одного и того же образца. После определения кальциевой жесткости pH образца уменьшают с помощью серной кислоты. Затем добавляются буфер Hardness 1 и ManVer 2, титрование выполняется с помощью TitraVer.

НЕ используйте эту процедуру, если для определения кальциевой жесткости использовался цианистый калий! Добавление серной кислоты вызовет выделение очень вредного газа цианистого водорода.

Колориметрический метод

Кальмагит, содержащийся в индикаторном растворе кальция и магния, добавляют к образцу и повышают pH примерно до 12,5 с помощью буфера. Добавление кальмагита перед корректировкой pH предотвращает осаждение кальция и магния, что типично при таком уровне pH. Затем проба делится на три равные части.

ЭДТА добавляется к первой порции для связывания кальция и магния, тем самым разрушая комплексы Ca / Mg-кальмагит. Этот раствор используется в качестве холостой пробы для стандартизации спектрофотометра. Длина волны измерения составляет 522 нм для спектрофотометров или 520 нм для колориметров.

EGTA (этиленгликоль-бис (β-аминоэтиловый эфир) -N, N, N ', N'-тетрауксусная кислота) добавляют во вторую порцию образца. EGTA избирательно хелатирует кальций; Остается измерить только оптическую плотность комплекса Mg-кальмагит. Результат выражается в мг/л Mg в виде CaCO3. 

Оптическая плотность третьей части образца (не содержащей хелатирующего агента) измеряется для определения мг/л Са в виде СаСО3. Обнулите спектрофотометр после измерения второй порции образца, чтобы компенсировать оптическую плотность ввиду наличия магния в образце.

Компания Hach Lange специализируется на производстве реагентов, лабораторных и промышленных приборов для анализа и контроля качетсва более 90 параметров воды 💧 с пошаговыми методиками выполнения тестов. АкваАналитикс® - официальный представитель Hach на территории России и стран СНГ. Для получения консультации по измерению интересующего вас параметра в лаборатории или на производстве свяжитесь с нами удобным для вас способом.

Представительство в России: +7 (495) 201-53-02 [email protected]

Представительство в Узбекистане: +998 (90) 174-57-84 [email protected]

Как определить жесткость воды в домашних условиях?

Москва

  • Главная
  • Блог
  • Как определить жесткость воды в домашних условиях?

Норма жесткости

По уровню жесткости вода делится на 3 категории (возьмем за основу «родные» градусы жесткости, °Ж):

  • мягкая: до 3°Ж
  • средняя по жесткости: 3–6°Ж
  • жесткая: >6°Ж

Определение жесткости воды в лаборатории

Это лучший способ узнать состав воды, ведь в лаборатории вам предоставят максимально точные данные.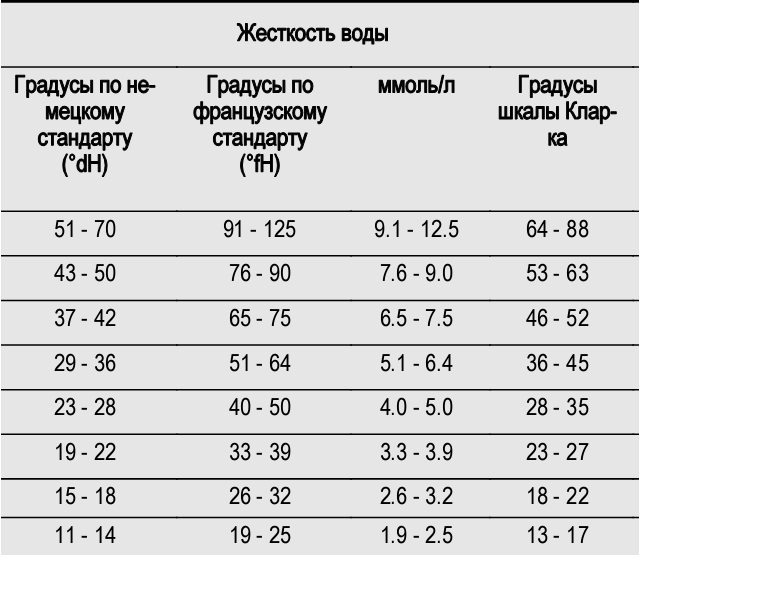 Например, в исследовательском центре АКВАФОР, который вошел в тройку лидеров среди сотен лабораторий России.

АКВАФОР DWM-101S Морион — абсолютная защита от любых вредных примесей, включая тяжелые металлы, нитраты и нитриты. Аналог бутилированной воды. Подходит аллергикам и новорожденным.

АКВАФОР Baby H Pro — система глубокой очистки и умягчения с абсолютной защитой от антибиотиков и гормонов.

АКВАФОР S800 (А800) — умягчение воды, удаление высоких концентраций железа и марганца.

Похожие статьи

  • 28 ноября 2018

    90

    Измеритель качества воды TDS-метр

  • 08 июля 2019

    92

    Лаборатория АКВАФОР взяла «серебро» по точности среди 53 лабораторий России

    • Наука

    • Новости

  • 24 января 2022

    65

    Можно ли смешивать кипяченую и некипяченую воду

  • 03 декабря 2021

    95

    Можно ли второй раз кипятить воду?

  • 16 ноября 2020

    79

    Лаборатория АКВАФОР: на страже вашего здоровья

    • Наука

    • Новости

  • 26 декабря 2018

    109

    Какая вода полезнее «кислотная» или «щелочная»?

  • 26 декабря 2018

    117

    Какой уголь подходит к фильтру для воды?

  • 15 апреля 2021

    90

    Запах сероводорода в воде из скважины

  • 04 октября 2022

    108

    Окислительно-восстановительный потенциал: влияет ли вода на старение?

Заявка на видеоконсультацию

1

мессенджер для связи

2

контактные данные

3

выбор даты

Заявка отправлена

Наш сотрудник проведет видеоконсультацию в выбранное время

Метод расчета жесткости и анализ характеристик жесткости болтовых соединителей

На этой странице

АннотацияВведениеРезультаты и обсуждениеЗаключениеДоступность данныхКонфликты интересовБлагодарностиСсылкиАвторское правоСтатьи по теме

В настоящее время немногие ученые изучали влияние шероховатости поверхности на жесткость сборки. Влиянием жесткости суставной поверхности на общую жесткость пренебрегают. В данной работе представлен новый метод расчета жесткости болтовых соединений. Рассмотрено влияние жесткости суставной поверхности на общую жесткость. Во-первых, изучается взаимосвязь между нагрузкой и перемещением между цилиндром и цилиндром (включая поверхность соединения с определенной шероховатостью) и получается характеристическое выражение жесткости поверхности соединения; результаты сравниваются с традиционной теорией расчета жесткости, а затем изучается влияние поверхности болтового соединения на болтовое соединение и сравнивается с результатами расчета жесткости традиционного болтового соединения. Результаты показывают, что теоретическая модель, представленная в этой статье, более практична.

1. Введение

Болтовое соединение является важным видом механического соединения. Он широко используется во всех видах механического соединения и играет очень важную роль в соединении механического оборудования. Поэтому необходимо изучить болтовое соединение. Жесткость болтового соединения также играет очень важную роль в конструкции станков.

Многие ученые изучали характеристики жесткости болтовых соединителей. Гомес и др. [1] изучали поведение разрушения при предварительном натягивании болта и обработке поверхности. Вилела и др. [2] выполнили численное моделирование болтового соединения. Некоторые ученые [3] разработали метод теоретического расчета жесткости болтовых соединителей. Некоторые ученые изучали характеристики жесткости болтовых соединителей, сочетая эксперимент с теорией. Некоторые ученые также использовали метод конечных элементов [4–8]. Педерсен проанализировал жесткость болтовых соединителей, а затем получил формулу для расчета жесткости болтовых соединителей путем подгонки.

Точер [9] предложил метод расчета жесткости болтовых соединителей. Он считал, что под давлением предварительно затянутых болтов в болтовых соединениях возникает зона влияния конической силы. В этом случае коэффициент жесткости на сжатие k элемента элементов может быть рассчитан по следующей формуле:

Метод расчета жесткости, предложенный Тохером [9], представляет собой метод расчета жесткости двух элементов в одинаковых условиях. Когда две толщины разные, каков метод расчета жесткости? В [8] Вильямс приводит метод расчета жесткости шарниров при этом условии. Формула для расчета жесткости элемента 1 (верхнего элемента) при предварительном натяжении болтами выглядит следующим образом:

Формулы расчета жесткости верхней части k элемента 21 элемента 2 (нижнего элемента) большей толщины и нижней части k элемента 22 элемента 2 (нижнего элемента) большей толщины можно соответственно , выраженная как

В соответствии с их соотношением, общая жесткость болтовых соединений может быть выражена как

Шигли и Мишке [10] также изучили формулу расчета жесткости болтовых соединений следующим образом:

Кроме того, все больше и больше ученых [11, 12] изучали смежные аспекты, такие как Juvinall и Marshek [13], и предлагали более простой метод расчета жесткости для оценки области зажима. Эта формула жесткости получается, когда зазор между болтом и соединителем очень мал.

Немецкая промышленная ассоциация (VDI) [14] предлагает формулу для расчета жесткости элементов. Приведены формулы для расчета жесткости стержней в двух разных случаях, что является пересмотром теории жесткости стержней Шигли и Мишке.

В дополнение к созданию теоретических моделей многие ученые провели анализ методом конечных элементов жесткости крепежных изделий и подобрали формулу расчета жесткости.

Сетураман и Кумар [15] использовали метод конечных элементов для анализа болтов двумя разными способами и подогнали формулу расчета жесткости.

Вайлман и др. [16] обнаружили, что жесткость болтовых элементов анализируется методом конечных элементов, а формула расчета жесткости подбирается исходя из предположения, что диаметр винта шайбового типа в 1,5 раза больше. Кроме того, Чжан и Пуарье [17] провели анализ методом конечных элементов и подобрали формулу расчета жесткости.

Все приведенные выше исследования жесткости болтовых соединений не учитывают влияние шероховатости поверхности на жесткость. Все они предполагают, что поверхность гладкая. В действительности поверхность обрабатываемых деталей имеет определенную шероховатость, которая не может быть гладкой. Следовательно, характеристики поверхности соединения, безусловно, будут влиять на жесткость болтовых соединений. В настоящее время проведено несколько связанных исследований, и влияние скованности суставов на общую скованность игнорировалось. Поэтому надо учиться. В данной статье представлен новый метод расчета жесткости болтовых соединений и рассмотрено влияние жесткости соединения на общую жесткость. Результаты предлагаемого метода сравниваются с результатами традиционного метода. Исследования в этой статье показывают, что теоретическая модель, представленная в этой статье, более практична. Структура этой статьи показана на рисунке 1.9.0003

2. Испытание поверхности соединения на жесткость
2.
1. Теория испытаний на жесткость поверхности соединения

Поскольку обработанная поверхность не является гладкой и состоит из ряда неровных пиков и впадин (как показано на рисунке 2), образующих определенную шероховатость, контакт двух шероховатых поверхностей образует поверхность соединения. Многие ученые изучали жесткость суставной поверхности: некоторые исследования основаны на теории фракталов [17–22] с микроперспективы, а некоторые ученые моделировали жесткость суставной поверхности на основе экспериментов. Формула характеристики жесткости получена по тесту [23–26]. Экспериментальные результаты показывают, что между нормальным давлением поверхности сустава и всесторонней деформацией микровыпуклого тела сустава существует следующая зависимость:

Формула (6) сдвигается, и получается производная. Связь между всесторонней деформацией и жесткостью микровыпуклого тела на поверхности соединения получается следующим образом:

Связь между контактным напряжением и жесткостью поверхности соединения может быть получена путем замены формулы (6) на формулу (7):

Учитывая интерфейс, состоящий из цилиндра 1 и цилиндра 2, как показано на рисунке 3, площадь интерфейса составляет S цилиндр 9. 0018 , высота цилиндра 1 равна H цилиндр 1 , модуль упругости E цилиндр 1 , высота цилиндра 2 H цилиндр 2 , модуль упругости цилиндра 2 E E Под действием нагрузки F нормальная полная деформация может быть выражена следующим образом:

Если материал двух контактных цилиндров одинаков, то есть E цилиндр1  =  E цилиндр21  =  E цилиндр , формула (9) может быть сокращена до

2.2. Экспериментальное испытание поверхности стыка

В этой статье планируется эксперимент, показанный на рис. 4. Экспериментальное устройство состоит из несущей рамы (фиксированной рамы), устройства предварительной затяжки болтов, механизма передачи нагрузки, датчика перемещения, датчика нагрузки. , дисплей смещения, дисплей нагрузки и провод передачи данных.

Модель датчика перемещения СПН-С4В, точность повторения используемого датчика перемещения 0,1  мк м. Точность срабатывания весового датчика составляет 1/1000, точность его передачи составляет 1/1000, а его диапазон составляет 0–300 кг.

Принцип измерения деформации поверхности соединения заключается в приложении крутящего момента к предварительно затянутому болту и преобразовании крутящего момента в нагрузку. Нагрузка передается от передаточного механизма на испытуемые детали и поверхности соединения. Нагрузка вызывает деформацию суставной поверхности. Датчик силы измеряет приложенную нагрузку, а датчик смещения измеряет деформацию суставной поверхности.

Материал экспериментальной заготовки – сталь 45 (рис. 5). Поверхность соединения обрабатывается фрезерованием на обрабатывающем центре с ЧПУ. При обработке поверхности заготовки скорость шпинделя обрабатывающего центра с ЧПУ составляет с  = 800 об/мин, скорость подачи обрабатывающего центра с ЧПУ составляет f  = 480 мм/мин, диаметр фрезерной головки составляет 120 мм, а радиус дуги режущей фрезы 1 мм. Известно, что шероховатость поверхности обрабатываемой детали составляет от 4,6 мкм, измеренная с помощью интерферометра белого света. При измерении поверхность соединения очищается, удаляются загрязнения и масло, а контакт между поверхностями соединения представляет собой контакт сухого трения.

2.3. Измерение модуля упругости материалов

Поскольку модуль упругости стали варьируется в определенном диапазоне, для конкретной стали, если требуется точно знать ее модуль упругости, его можно получить только методом испытаний.

Стандартные детали для испытаний на модуль упругости изготавливаются из той же партии материалов, что и испытания на деформацию, описанные выше, а затем проводятся испытания на растяжение на прецизионной машине для испытаний на растяжение (рис. 6) для определения модуля упругости материалов и в процессе тестирования используется прецизионный экстензометр. Материал был разорван во время теста (рис. 7).

Используемая модель машины для испытания материалов на растяжение — DNS600, а ее максимальная растягивающая нагрузка может достигать 60 тонн. Материал приспособления представляет собой гидравлическое приспособление. Начальная зажимная нагрузка составляет 1000 Н. При продолжении процесса растяжения зажимная нагрузка гидравлического приспособления быстро увеличивается, и окончательная зажимная нагрузка намного превышает 1000 Н. Поэтому, когда материал разрывается (рис. 7), зажимная нагрузка намного превышает 1000 Н. Следовательно, мы видим, что материал зажимается в плоскую форму (рис. 7).

В процессе измерения используется модель экстензометра CBY1 50-5, его точность может достигать 1/10000, а погрешность измерения составляет 1/100.

Материал стандарта испытаний - сталь 45, а химический состав стали C45 следующий: 0,45% C, 0,04% S, 0,25% Si, макс. 0,3% Cr, макс. 0,3% Ni, 0,65% Mn, макс. 0,3 % Cu и 0,04 % P [27].

Модуль упругости материала можно рассчитать по диаграмме нагрузки-деформации реального устройства (рис. 8), если диаметр материала и длина заготовки известны и измерены с помощью экстензометра.

2.4. Экспериментальный результат

Из рисунка 8 можно рассчитать модуль Юнга E  = 200 ГПа стали 45, а затем подставить его в формулу (10). Затем измеренные данные аппроксимируются с помощью Matlab, чтобы ошибка между кривой и экспериментальными данными была как можно меньше. Как показано на Рисунке 9, характерное соотношение между деформацией и давлением поверхности подогнанного сустава выглядит следующим образом:

Соотношение между жесткостью сустава и давлением выглядит следующим образом:

Как показано на рисунке 9, экспериментальное значение сравнивается с теоретическим значением. Из рисунка 9 видно, что экспериментальная кривая хорошо согласуется с теоретической кривой аппроксимации, а погрешность немного велика в пределах 500 N. весь.

3. Анализ влияния жесткости поверхности соединения
3.1. Цилиндры и их соединительная поверхность

Материал цилиндра — сталь 45, модуль упругости — 200 000 МПа. Как показано на рисунке 10, высота цилиндра 1 равна H 1  = 30 мм, а у цилиндра 2 H 1  = 23 мм. Нормальная (осевая) жесткость на сжатие двух структур изучается для изучения влияния характеристик поверхности соединения на общую осевую жесткость.

Как видно из рисунка 11, результаты традиционного метода без учета влияния шероховатости поверхности больше, чем у предлагаемого метода.

С увеличением нагрузки на поверхность стыка результаты расчетов по представленной в статье методике постепенно увеличиваются и постепенно приближаются к результатам расчетов по традиционной теории.

Для дальнейшего изучения влияния жесткости шероховатости поверхности на общую жесткость толщину верхнего элемента H цилиндр1  = 23 мм, H цилиндр2  = 18 18 5мм,  = 18 18 мм, цилиндр3  = 13 мм, H цилиндр4  = 8 мм соответственно. Значения других параметров такие же, как и раньше. Модуль упругости материала E цилиндра  = 200000 МПа, диаметр цилиндра R цилиндр  = 20 мм, а нормальные характеристические параметры шероховатости поверхности стыка получены из экспериментов.

Исследовано влияние характеристик шероховатой поверхности соединения на жесткость болтовых соединений. Толщина элементов одинаковая, все они 60 мм, диаметр болтов 10 мм, диаметр элементов 11 мм. Традиционный метод расчета жесткости элементов сравнивается с текущим методом расчета. Материал элементов - сталь 45, а ширина элемента достаточна для болтового соединения, чтобы сформировать конус влияния.

3.2. Болтовые элементы и их соединительная поверхность

Для дальнейшего изучения влияния жесткостных характеристик черновых соединений на болтовые соединения разработаны следующие схемы исследований: как показано на рисунке 12, используются болты М10 с диаметром отверстий под болты 11 мм. и толщина болтовых соединений составляет T Meman11 = T Meman2 = 5 мм, T Meman1 = T Member2 = 10 мм, T Member2 = 10 мм, T .0015 T Member1 = T Meman2 = 15 мм и T Meman1 = T Member2 = 20 мм соответственно. В соответствии с теорией конуса влияния можно рассчитать основные несущие области соединений, а модуль упругости материалов элементов составляет 200 000 МПа. Результаты анализа представлены на рисунке 13.

3.3. Влияние шайбы и поверхности соединения

Для изучения влияния элемента на общую жесткость разработана исследовательская модель, показанная на рисунке 14. Толщина двух элементов составляет 25 мм. Для соединения элементов используются болты М10. Модуль упругости материала элемента равен 9.0015 E  = 200 000 МПа. Длина и ширина элементов 100 мм. Диаметр отверстий под болты элементов составляет 11 мм. Болты имеют стандартные характеристики.

Существует два способа соединения: один — установка элемента на конец гайки, а другой — установка элемента на головку болта и конец гайки соответственно.

4. Результаты и обсуждение

На рис. 11 показано, что при условии равномерной нормальной нагрузки результаты, рассчитанные традиционным методом, больше, чем полученные экспериментально. Следовательно, это показывает, что жесткость шероховатой поверхности, образованной обработанной поверхностью, оказывает определенное влияние на общую жесткость оборудования. Неразумно, чтобы жесткость, рассчитанная традиционным методом, не учитывала влияние шероховатости поверхности на жесткость. Результаты показывают, что жесткость соединения снижает общую жесткость механизма.

Как видно из рисунка 11, результаты традиционного метода без учета влияния шероховатости поверхности больше, чем у предлагаемого метода. С увеличением нагрузки на поверхность стыка результаты расчетов по представленной в статье методике постепенно увеличиваются и постепенно приближаются к результатам расчетов по традиционной теории.

На рис. 15 показано, что когда цилиндр подвергается равномерной нагрузке, высота цилиндра влияет на общую жесткость. Эффект заключается в том, что общая жесткость увеличивается с уменьшением толщины, но это увеличение относительно небольшое.

На рисунке 16 показано, что для болтовых соединений с шероховатой поверхностью расчетные значения традиционной теории больше, чем те, которые используются в настоящей теории. Характеристики жесткости шероховатых соединений влияют на общую жесткость конструкции. С увеличением нормальной нагрузки общая жесткость постепенно увеличивается и постепенно приближается к традиционному теоретическому расчетному значению. Чем больше нормальная нагрузка, тем ближе расчетное значение этого метода к традиционному расчетному значению.

На рис. 13 показано, что чем толще болтовое соединение, тем выше общая жесткость. Это противоречит выводу о равномерно нагруженных цилиндрических элементах (рис. 15). Из рисунка 13 видно, что общая жесткость равномерно нагруженных цилиндрических элементов уменьшается с увеличением толщины элементов. Эти два вывода противоположны, потому что эффективная площадь поверхности раздела между болтовыми элементами и элементами уменьшается с толщиной элементов, поэтому жесткость интерфейса между элементами и элементами уменьшается. Хотя толщина элементов уменьшается, жесткость элементов увеличивается, но это увеличение происходит медленно, то есть жесткость соединений без элементов быстро уменьшается, поэтому чем толще конструкция, тем больше общая жесткость.

Как видно из рисунка 17, жесткость обоих болтов увеличивается с увеличением предварительного натяга болта, а скорость изменения уменьшается с увеличением нагрузки.

Из рисунка 17 видно, что жесткость одного элемента больше, чем у двух элементов. При одинаковом предварительном натяге жесткость одного элемента намного больше, чем у двух элементов, что указывает на то, что количество элементов оказывает большее влияние на общую жесткость.

5. Заключение

Модель расчета, предложенная в этой статье, более практична, чем в предыдущем методе. Результаты показывают, что жесткостные характеристики шероховатости обработанной поверхности оказывают большое влияние на общую жесткость. Чем больше количество поверхностных соединений, тем меньше общая жесткость конструкции и тем легче конструкция деформируется.

Исследование также показывает, что жесткость соединения и всей конструкции увеличивается с увеличением усилия предварительной затяжки болта, и чем больше усилие предварительной затяжки, тем выше общая жесткость. Результаты также показывают, что зазор между соединениями снижает жесткость болтовых соединений. В данной работе теоретически подтверждается гипотеза о том, что чем больше усилие предварительного натяжения болта, тем больше жесткость конструкции, тем больше поверхность соединения и меньше жесткость механизма.

Nomenclature
k member : Overall stiffness of members (N/m)
L member-total : Total thickness of members (m)
E member : Young's modulus of members (Pa)
D hole : Member hole diameter (m)
d washer : Diameter of washer (m)
α : Influencing cone angle (radian)
k member1 : Stiffness of member1 (N/m)
E member1 : Young's modulus of member1 (Pa)
d bolt : Bolt diameter (m)
k member21 : Stiffness of the first part of member2 (N/m)
E member2 : Young's modulus of member2 (Pa)
t member2 : Толщина члена2 (мм)
T Meman1 : Толщина Mempor1 (MM)
K 9 24262 9026. : Second Member
.: neckers of
.
k
k
al.
. )
λ joint : Deformation of joint surface (mm)
m normal : Normal characteristic parameters of joint surface
c normal : Нормальные характеристические параметры суставной поверхности
p норма : Нормальное давление суставной поверхности (Па)
k СОВЕТ : ГРЕЙСТВА СВЕДЕНИЯ СВОИХ (N/M)
S Цилиндр : Площадь цилиндрического сустава (M 2 ). : Height of cylinder1 (m)
E cylinder1 : Elastic modulus of cylinder1 (Pa)
H cylinder2 : Height of cylinder2 (m)
E cylinder2 : Elastic modulus of cylinder2 (Pa)
E cylinder : Modulus of elasticity of cylinder (Pa)
k cylinder : Жесткость цилиндра (Н/м)
с цилиндр : Площадь соединения (м 2 ).
Доступность данных

Данные, использованные для подтверждения результатов этого исследования, включены в статью.

Конфликт интересов

Авторы заявляют об отсутствии конфликта интересов.

Благодарности

Авторы благодарят за поддержку Национальный фонд естественных наук Китая (гранты № 51675422, 51475366 и 51475146) и Проект планирования науки и технологий провинции Шэньси (грант № 2016JM5074).

Ссылки

  1. В. Гомес, М. Родригес, Х. Коррейя, М. Фигейредо, А. де Хесус и А. Фернандес, «Монотонное поведение и разрушение болтовых соединений с различными предварительными нагрузками болтов и обработкой поверхности», Frattura Ed Integrità Strutturale , vol. 13, нет. 48, стр. 304–317, 2019.

    Посмотреть по адресу:

    Сайт издателя | Google Scholar

  2. P. M. L. Vilela, H. Carvalho и O. T. Baião Filho, «Численное моделирование болтовых соединений», Latin American Journal of Solids and Structures , том. 15, нет. 10, 2018.

    Посмотреть по адресу:

    Google Scholar

  3. Н. Хайдар, С. Обид и М. Джавад, «Математическое представление жесткости болтового соединения: новая предлагаемая модель», Journal of Mechanical Science и технологии , вып. 25, нет. 11, стр. 2827–2834, 2011.

    Посмотреть по адресу:

    Сайт издателя | Google Scholar

  4. Н. С. Аль-Хунити и С. Насер, «Расчет жесткости стержня в болтовых соединениях с использованием анализа методом конечных элементов», Проектирование конструкций и машин на основе механики , вып. 33, нет. 3–4, стр. 331–342, 2005 г.

    Посмотреть по адресу:

    Сайт издателя | Google Scholar

  5. Н. Л. Педерсен и П. Педерсен, «Об анализе жесткости предварительно напряженных контактных узлов болт-пластина», Archive of Applied Mechanics , vol. 78, нет. 2, стр. 75–88, 2008 г.

    Посмотреть по адресу:

    Сайт издателя | Google Scholar

  6. Г. Ян, Дж. Хонг, Н. Ван, Л. Чжу, Ю. Дин и З. Ян, «Жесткость элементов и контактные характеристики интерфейса болтовых соединений», в Proceedings of the IEEE International Symposium on Assembly & Manufacturing IEEE , Тампере, Финляндия, май 2011 г.

    Просмотр по адресу:

    Google Scholar контактные узлы №», Проектирование конструкций и машин на основе механики , том. 36, нет. 1, стр. 47–66, 2008 г.

    Посмотреть по адресу:

    Сайт издателя | Google Scholar

  7. Дж. Уайлман, М. Чоудхури и И. Грин, «Расчет жесткости стержня в болтовых соединениях», Журнал механического проектирования , том. 113, нет. 4, с. 432, 1991.

    Посмотреть по адресу:

    Сайт издателя | Google Scholar

  8. A. Yamamoto, The Theory and Computation of Thread Connection , Yokendo, Tokyo, Japan, 1980.

  9. J. E. Shigley and C. R. Mischke, Mechanical Engineering Design, McGraw 9001 , Нью-Йорк, США, 5-е издание, 1989 г.

  10. Т. Ф. Ленхофф, М. Л. Маккей и В. А. Беллора, «Жесткость элементов и расстояние между болтами болтовых соединений», Американское общество инженеров-механиков , vol. 248, стр. 63–72, 1992.

    Просмотр по адресу:

    Google Scholar

  11. А. Н. Шербурн и М. Р. Бахаари, «Конечно-элементный прогноз поведения торцевых пластин с болтовым соединением. I: параметрическое исследование», Journal of Structural Engineering , vol. 123, нет. 2, стр. 157–164, 1997.

    Посмотреть по адресу:

    Сайт издателя | Google Scholar

  12. Р. К. Джувиналл и К. М. Маршек, Fundamentals of Machine Design , John Wiley & Sons, Хобокен, Нью-Джерси, США, 2-е издание, 1991 г.

  13. V. D. Ingenieure, Систематический расчет высокопрочных болтовых соединений с одним цилиндрическим болтом , Окриджская национальная лаборатория, Ок-Ридж, Теннесси, США, 2003.

  14. Р. Сетураман и Т. С. Кумар, «Оценка жесткости осесимметричных болтовых соединений на основе конечных элементов», Journal of Mechanical Design , vol. 131, нет. 1, 2009 г..

    Посмотреть по адресу:

    Сайт издателя | Google Scholar

  15. Дж. Г. Уильямс, Р. Э. Энли, Д. Х. Нэш и Т. Г. Ф. Грей, «Анализ болтовых соединений с внешней нагрузкой: аналитическое, расчетное и экспериментальное исследование», International Journal of Pressure Vessels and Piping , vol. 86, нет. 7, стр. 420–427, 2009 г.

    Посмотреть по адресу:

    Сайт издателя | Google Scholar

  16. О. Чжан и Ж. А. Пуарье, «Новая аналитическая модель болтовых соединений», Журнал механического проектирования , том. 126, нет. 4, стр. 721–728, 2004.

    Посмотреть по адресу:

    Сайт издателя | Google Scholar

  17. Ян Х., «Расчетная модель нормальной контактной жесткости соединений на основе фрактальной геометрии и теории контакта», Journal of Machine Engineering , vol. 49, нет. 1, с. 102, 2013.

    Посмотреть по адресу:

    Сайт издателя | Google Scholar

  18. Дж. Ф. Шен, К. Х. Ву и Ф. Ян, «Фрактальная геометрическая модель нормальной контактной жесткости, основанная на гамма-распределении шероховатой поверхности соединения», Advanced Materials Research , vol. 760–762, стр. 2064–2067, 2013.

    Посмотреть по адресу:

    Сайт издателя | Google Scholar

  19. К. Чжай, С. Беванд, Ю. Ган и др., «Измерение нормальной контактной жесткости фрактальных шероховатых поверхностей», 2014 г. , https://arxiv.org/abs/1408.6272.

    Просмотр по адресу:

    Google Scholar

  20. Ю. Чен, С. Чжан, С. Вэнь, Г. Лан, Ю. Ван и С. Фан, «Упругопластический контакт с шероховатой поверхностью, непрерывная гладкая экспоненциальная функциональная модель и нормальная контактная жесткость», Журнал Сианьского университета Цзяотун , том. 50, нет. 7, pp. 58–67, 2016.

    Просмотр по адресу:

    Google Scholar

  21. W. Pan, X. Li, L. Wang, N. Guo, and J. Mu, «Фрактал нормальной контактной жесткости модель прогнозирования шероховатой поверхности при сухом трении и экспериментальная проверка», European Journal of Mechanics-A/Solids , vol. 66, стр. 94–102, 2017.

    Посмотреть по адресу:

    Сайт издателя | Google Scholar

  22. Ю. Хуан и В. Фу, «Исследование нормальных динамических характеристик суставной поверхности», Журнал машиностроения , том. 29, нет. 3, pp. 74–78, 1993.

    Просмотр по адресу:

    Google Scholar

  23. Ю. Хуанг, В. Фу и С. Ян, «Методы получения практических параметров тангенциального демпфирования поверхностей соединения», Журнал Сианьского технологического университета , том. 12, нет. 1, стр. 1–5, 1996.

    Просмотр по адресу:

    Google Scholar

  24. С. Ван, Ю. Лей, С. Сяси, З. Цзиньцзюань и Х. Юмей, «Характеристики демпфирования чугуна поверхность в контакте нормальная», Труды Китайского общества сельскохозяйственной техники , том. 44, нет. 12, pp. 321–325, 2013.

    Просмотр по адресу:

    Google Scholar

  25. Х. Йе, Ю. Хуан, П. Ли, Ю. Ли и Л. Бай, «Сбор параметров виртуального материала на основе по основным характеристикам интерфейсов болтовых соединений», Tribology International , vol. 95, стр. 109–117, 2016.

    Посмотреть по адресу:

    Сайт издателя | Google Scholar

  26. М. Шкодо, «Взаимосвязь между микроструктурой стали С45, легированной лазером, и ее кавитационной стойкостью», Журнал технологии обработки материалов , том. 162-163, вып. 20, стр. 410–415, 2005.

    Посмотреть по адресу:

    Сайт издателя | Google Scholar

Copyright

Copyright © 2019 Shi-kun Lu et al. Это статья с открытым доступом, распространяемая в соответствии с лицензией Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии надлежащего цитирования оригинальной работы.

Аналитическое определение жесткости при изгибе пятислойного гофрированного картона с дефектами

1. Баум Г.А., Бреннан Д.К., Хабегер К.К. Ортотропные упругие константы бумаги. Таппи. 1981; 64: 97–101. [Google Scholar]

2. Mann R.W., Baum G.A., Habeger C.C. Определение всех девяти ортотропных упругих постоянных для бумаги машинного производства. Таппи. 1980; 63: 163–166. [Google Scholar]

3. Фрэнк Б. Сжатие гофрированных коробок. Обзор литературы. Упак. Технол. науч. 2014; 27:105–128. doi: 10.1002/pts.2019. [CrossRef] [Google Scholar]

4. Zhang Y.-L., Chen J., Wu Y., Sun J. Анализ факторов опасности использования гофрокартона в упаковке низкотемпературного йогурта при логистике. Procedia Окружающая среда. науч. 2011;10:968–973. doi: 10.1016/j.proenv.2011.09.155. [CrossRef] [Google Scholar]

5. Хун Д., Накано Ю., Танака Ф., Хаманака Д., Учино Т. Сохранение прочности гофрокартона в условиях повышенной влажности с помощью наноразмерных аэрозолей. Композиции науч. Технол. 2010;70:2123–2127. doi: 10.1016/j.compscitech.2010.08.011. [CrossRef] [Google Scholar]

6. Галло Дж., Кортес Ф., Альберди Э., Готи А. Моделирование механического поведения контейнеров и октабинов из гофрированного картона, подвергающихся вертикальным нагрузкам при штабелировании. Материалы. 2021;14:2392. doi: 10.3390/ma14092392. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

7. Бороч П., Молнар Б. Измерение и анализ уровней вибрации в уложенных штабелями мелких посылок в автофургонах в зависимости от свободного пространства для движения. заявл. науч. 2020;10:7821. doi: 10.3390/app10217821. [CrossRef] [Google Scholar]

8. Quesenberry C., Horvath L., Bouldin J., White M.S. Влияние жесткости верхнего настила поддона на прочность на сжатие асимметрично поддерживаемых коробок из гофрированного картона. Упак. Технол. науч. 2020; 33: 547–558. doi: 10.1002/pts.2533. [Перекрестная ссылка] [Академия Google]

9. Гарбовский Т. , Гаевский Т., Грабский Ю.К. Оценка прочности на сжатие коробок из гофрокартона с различными отверстиями. Энергии. 2021;14:155. doi: 10.3390/en14010155. [CrossRef] [Google Scholar]

10. Garbowski T., Gajewski T., Grabski J.K. Оценка прочности на сжатие коробок из гофрокартона с различной перфорацией. Энергии. 2021;14:1095. doi: 10.3390/en14041095. [CrossRef] [Google Scholar]

11. Гарбовски Т., Книттер-Пятковска А., Мрувчиньски Д. Численная гомогенизация многослойного гофрокартона с биговкой или перфорацией. Материалы. 2021;14:3786. дои: 10.3390/ma14143786. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

12. Гун Г., Лю Ю., Фан Б., Сунь Д. Деформация и прочность на сжатие гофрокартона при различных формах вдавливания: экспериментальное и имитационное исследование . Упак. Технол. науч. 2020; 33: 215–226. doi: 10.1002/pts.2499. [CrossRef] [Google Scholar]

13. Fadiji T., Coetzee C.J., Opara U.L. Прочность на сжатие упаковок из вентилируемого гофрированного картона: численное моделирование, экспериментальная проверка и влияние геометрического дизайна вентиляционных отверстий. Биосист. англ. 2016; 151: 231–247. doi: 10.1016/j.biosystemseng.2016.090,010. [CrossRef] [Google Scholar]

14. Fadiji T., Ambaw A., Coetzee C.J., Berry T.M., Opara U.L. Применение анализа методом конечных элементов для прогнозирования механической прочности упаковки из вентилируемого гофрированного картона для обработки свежих продуктов. Биосист. англ. 2018; 174: 260–281. doi: 10.1016/j.biosystemseng.2018.07.014. [CrossRef] [Google Scholar]

15. Мрувчиньски Д., Гарбовски Т., Книттер-Пятковска А. Оценка прочности на сжатие коробок из гофрокартона со смещенными складками на клапанах. Материалы. 2021;14:5181. дои: 10.3390/ma14185181. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

16. Тутак Д., Кескин Б., Абубакр С., Флеминг П.Д. Исследование влияния офсетной краски на основе каучука, нанесенной на упаковочный картон, на прочностные свойства упаковочного картона. Междунар. Дж. Заявл. науч. Технол. 2019;9:9–17. doi: 10.30845/ijast.v9n3p2. [CrossRef] [Google Scholar]

17. Kellicutt K., Landt E. Разработка проектных данных для морских контейнеров из гофрированного картона. Таппи Дж. 1952; 35: 398–402. [Академия Google]

18. Allerby I.M., Laing G.N., Cardwell R.D. Прочность на сжатие — от компонентов до гофрированных контейнеров. Аппита конф. Ноты. 1985: 1–11. [Google Scholar]

19. Шрампфер К.Э., Уитситт В.Дж., Баум Г.А. Комбинированная технология Board Edge Crush (ECT). Институт химии бумаги; Appleton, WI, USA: 1987. [Google Scholar]

20. Batelka J.J., Smith C.N. Пакетная модель сжатия. Институт Бумаги Науки и Технологии; Атланта, Джорджия, США: 1993. [Google Scholar]

21. Урбаник Т.Дж., Франк Б. Анализ сжатия данных со всего мира за 46 лет. Наука о древесном волокне. 2006; 38: 399–416. [Google Scholar]

22. Захир М., Авайс М., Рауткари Л., Сорвари Дж. Анализ методом конечных элементов картонной упаковки под сжимающей нагрузкой. Процедиа Мануф. 2018;17:1162–1170. doi: 10.1016/j.promfg.2018.10.008. [CrossRef] [Google Scholar]

23. Garbowski T., Gajewski T., Grabski J.K. Роль коробления при оценке прочности на сжатие коробок из гофрированного картона. Материалы. 2020;13:4578. дои: 10.3390/ma13204578. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

24. Чеховский Л., Беньковска М., Шевчик В. Разрушение картонных труб из-за бокового сжатия — экспериментальное и численное исследование. Композиции Структура 2018;203:132–141. doi: 10.1016/j.compstruct.2018.07.027. [CrossRef] [Google Scholar]

25. Гарбовски Т., Ярмущак М. Численная оценка прочности упаковок из гофрокартона. Часть 1. Теоретические допущения при численном моделировании картонных упаковок. пол. Пап. Ред. 2014; 70:219–222. (на польском языке) [Google Scholar]

26. Гарбовски Т., Ярмущак М. Численная оценка прочности упаковок из гофрокартона. Часть 2. Экспериментальные испытания и численный анализ картонных упаковок. пол. Пап. 2014; 70: 277–281. (на польском языке) [Google Scholar]

27. Пак Дж., Чанг С., Юнг Х.М. Численное прогнозирование эквивалентных механических свойств гофрированного картона с помощью трехмерного конечно-элементного анализа. заявл. науч. 2020;10:7973. doi: 10.3390/app10227973. [Перекрестная ссылка] [Академия Google]

28. Пак Дж., Пак М., Чой Д.С., Юнг Х.М., Хван С.В. Моделирование на основе конечных элементов поведения гофрированного картона при поперечном сжатии для упаковки сельскохозяйственной продукции. заявл. науч. 2020;10:6716. doi: 10.3390/app10196716. [CrossRef] [Google Scholar]

29. Чеховский Л., Кмита-Фудалей Г., Шевчик В., Гралевски Ю., Беньковска М. Численное и экспериментальное исследование жесткости пятислойной несимметричной картонной панели. Материалы. 2021;14:7453. doi: 10.3390/ma14237453. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

30. Джамсари М.А., Кюэ С., Грей-Стюарт Э.М., Дам К., Бронлунд Дж.Э. Экспериментальные и численные характеристики гофрокартона при различных ориентациях при испытании на четырехточечный изгиб. Упак. Технол. науч. 2019; 32: 555–565. doi: 10.1002/pts.2471. [CrossRef] [Google Scholar]

31. Урбаник Т.Дж., Саликлис Е. П. Конечно-элементное подтверждение явления коробления, наблюдаемого в гофрированных коробках. Наука о древесном волокне. 2003; 35: 322–333. [Google Scholar]

32. Nordstrand T. Ph.D. Тезис. Лундский университет; Лунд, Швеция: 2003 г. Основные испытания и расчет прочности гофрированного картона и контейнеров. [Академия Google]

33. Нордстранд Т., Карлссон Л. Оценка поперечной жесткости сэндвич-панелей с наполнителем. Композиции Структура 1997; 37: 145–153. doi: 10.1016/S0263-8223(97)80007-4. [CrossRef] [Google Scholar]

34. Гарбовски Т., Гаевски Т. Определение жесткости сэндвич-панелей с гофрированным заполнителем при поперечном сдвиге методом численной гомогенизации. Материалы. 2021;14:1976. doi: 10.3390/ma14081976. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

35. Авилес Ф., Карлссон Л.А., Мэй-Пэт А. Состав многослойного скрученного образца с поправкой на сдвиг. Эксп. мех. 2012; 52:17–23. doi: 10.1007/s11340-011-9501-4. [CrossRef] [Google Scholar]

36. Слонина М., Дзюрка Д., Смардзевски Дж. Экспериментальное исследование и численный анализ упругих свойств бумажных ячеек до и после пропитки. Материалы. 2020;13:2058. doi: 10.3390/ma13092058. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

37. Доманески М., Перего У., Боргквист Э., Борсари Р. Ориентированная на отрасль стратегия конечно-элементного моделирования биговки и фальцовки картона. Упак. Технол. науч. 2017;30:269–294. doi: 10.1002/pts.2298. [CrossRef] [Google Scholar]

38. Авайс М., Таннинен П., Леппянен Т., Мэтьюз С., Сорвари Дж., Варис Дж., Бэкфол К. Расчетный и экспериментальный анализ поведения складок в процессе штамповки . Процедиа Мануф. 2018;17:835–842. doi: 10.1016/j.promfg.2018.10.135. [CrossRef] [Google Scholar]

39. Thakkar B.K., Gooren L.G.J., Peerlings R.H.J., Geers M.G.D. Экспериментальное и численное исследование сминаемости гофрированного картона. Филос. Маг. 2008;88:3299–3310. doi: 10.1080/14786430802342576. [CrossRef] [Google Scholar]

40. Beex L.A.A., Peerlings R.H.J. Экспериментальное и компьютерное исследование биговки и складывания ламинированного картона. Междунар. J. Структура твердых тел. 2009; 46:4192–4207. doi: 10.1016/j.ijsolstr.2009.08.012. [CrossRef] [Google Scholar]

41. Giampieri A., Perego U., Borsari R. Конструктивная модель механической реакции на складывание гофрированного картона. Междунар. J. Структура твердых тел. 2011;48:2275–2287. doi: 10.1016/j.ijsolstr.2011.04.002. [Перекрестная ссылка] [Академия Google]

42. Леминена В., Таннинена П., Песонена А., Варис Дж. Влияние механической перфорации на процесс штамповки картона. Процедиа Мануф. 2019; 38: 1402–1408. doi: 10.1016/j.promfg.2020.01.148. [CrossRef] [Google Scholar]

43. Бьянколини М.Е. Оценка эквивалентных жесткостных свойств гофрированного картона. Композиции Структура 2005; 69: 322–328. doi: 10.1016/j.compstruct.2004.07.014. [CrossRef] [Google Scholar]

44. Гарбовски Т., Ярмущак М. Гомогенизация гофрированного картона. Часть 1. Аналитическая гомогенизация. пол. Пап. 2014; 70:345–349.. (на польском языке) [Google Scholar]

45. Гарбовски Т., Ярмущак М. Гомогенизация гофрированного картона. Часть 2. Численная гомогенизация. пол. Пап. 2014; 70:390–394. (на польском языке) [Google Scholar]

46. Гарбовски Т., Марек А. Гомогенизация гофрокартона методом обратного анализа; Материалы 1-й Международной конференции по оптимизации инженерных и прикладных наук; Остров Кос, Греция. 4–6 июня 2014 г.; стр. 1751–1766. [Google Scholar]

47. Hohe J. Метод прямой гомогенизации для определения матрицы жесткости микрогетерогенных плит применительно к сэндвич-панелям. Композиции Часть Б англ. 2003; 34: 615–626. дои: 10.1016/S1359-8368(03)00063-5. [CrossRef] [Google Scholar]

48. Buannic N., Cartraud P., Quesnel T. Гомогенизация сэндвич-панелей с гофрированным наполнителем. Композиции Структура 2003; 59: 299–312. doi: 10.1016/S0263-8223(02)00246-5. [CrossRef] [Google Scholar]

49. Abbes B. , Guo Y.Q. Аналитическая гомогенизация для кручения ортотропных сэндвич-панелей: Заявка . Композиции Структура 2010;92:699–706. doi: 10.1016/j.compstruct.2009.09.020. [CrossRef] [Google Scholar]

50. Марек А., Гарбовски Т. Гомогенизация сэндвич-панелей. вычисл. Ассистент Методы инж. науч. 2015;22:39–50. [Google Scholar]

51. Суарес Б., Мунета М.Л.М., Санс-Боби Дж.Д., Ромеро Г. Применение подходов гомогенизации к численному анализу сидений из многослойного гофрированного картона. Композиции Структура 2021;262:113642. doi: 10.1016/j.compstruct.2021.113642. [CrossRef] [Google Scholar]

52. Nguyen-Minh N., Tran-Van N., Bui-Xuan T., Nguyen-Thoi T. Статический анализ гофрированных панелей с использованием моделей гомогенизации и сглаженной пластины Mindlin на основе клеток. элемент (CS-MIN3) Фронт. Структура Гражданский англ. 2019;13:251–272. doi: 10.1007/s11709-017-0456-0. [CrossRef] [Google Scholar]

53. Аллауи С., Бензеггаг М.Л., Абура З., Талби Н. Упругое поведение гофрированного картона: эксперименты и моделирование. Композиции Структура 2004; 63: 53–62. [Google Scholar]

54. Рамирес-Торрес А., Ди Стефано С., Грилло А., Родригес-Рамос Р., Меродио Дж., Пента Р. Подход асимптотической гомогенизации к микроструктурной эволюции гетерогенных сред. Междунар. Дж. Нон-Лин. мех. 2018; 106: 245–257. doi: 10.1016/j.ijnonlinmec.2018.06.012. [Перекрестная ссылка] [Академия Google]

55. Рамирес-Торрес А., Пента Р., Родригес-Рамос Р., Меродио Х., Сабина Ф.Х., Браво-Кастильеро Х., Гиноварт-Диас Р., Прециози Л., Грилло А. Асимптотическая гомогенизация по трем шкалам и его применение к многослойным иерархическим твердым тканям. Междунар. J. Структура твердых тел. 2018;130:190–198. doi: 10.1016/j.ijsolstr.2017.09.035. [CrossRef] [Google Scholar]

56. Гарбовски Т., Грабски Дж. К., Марек А. Измерения полного поля при испытании на сжатие кромки гофрированного картона — аналитические и численные прогностические модели. Материалы. 2021;14:2840. дои: 10.3390/ma14112840. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

57. Garbowski T., Knitter-Piątkowska A., Marek A. Новая конфигурация испытания на сжатие краев, дополненная измерениями деформации в полном поле. Материалы. 2021;14:5768. doi: 10.3390/ma14195768. [Бесплатная статья PMC] [PubMed] [CrossRef] [Google Scholar]

58. Hägglund R., Åslund P.E., Carlsson L.A., Isaksson P. Измерение изменений толщины панелей из гофрированного картона, нагруженных сжатием по краям, с использованием корреляции цифровых изображений. Дж. Сэндв. Структура Матер. 2010; 14:75–794. doi: 10.1177/1099636211419133. [CrossRef] [Google Scholar]

59. Вигье Ж., Дюмон П.Ж.Ж., Ваше П., Оржеас Л., Деслог И., Море Э. Анализ поля деформации и напряжения картонной коробки во время сжатия с помощью трехмерной корреляции цифровых изображений. . заявл. мех. Матер. 2010;24–25:103–108. doi: 10.4028/www.scientific.net/AMM.24-25.103. [CrossRef] [Google Scholar]

60. Вигье Ж., Дюмон П.Ж.Ж., Оргеас Л., Ваше П., Деслог И., Море Э. Поля поверхностных напряжений и деформаций на сжатых панелях ящиков из гофрокартона. Экспериментальный анализ с использованием стереокорреляции цифрового изображения. Композиции Структура 2011;93: 2861–2873. doi: 10.1016/j.compstruct.2011.05.018. [CrossRef] [Google Scholar]

61. Viguié J., Dumont P.J.J. Аналитическая модель панелей из гофрированного картона после деформации с использованием измерений корреляции цифровых изображений. Композиции Структура 2013; 101: 243–254. doi: 10.1016/j.compstruct.2013.01.023. [CrossRef] [Google Scholar]

62. Гарбовски Т., Майер Г., Новати Г. О калибровке ортотропных упруго-пластических конститутивных моделей для бумажной фольги с помощью двухосных испытаний и обратного анализа. Структура Мультидиск. Оптим. 2012;46:111–128. doi: 10.1007/s00158-011-0747-3. [Перекрестная ссылка] [Академия Google]

63. Фадиджи Т., Кутзи С.Дж., Опара У.Л. Оценка поля смещения картонных упаковок, подвергнутых компрессионной нагрузке, с использованием цифровой корреляции изображений (DIC) Food Bioprod.

Learn more