Как узнать угол наклона лестницы в градусах
Угол наклона лестницы - инструкция как рассчитать оптимальный угол наклона лестницы на второй этаж, ГОСТ, видео
Подобрать эргономичный и комфортный угол наклона — это одна из основных задач при конструировании лестницы. Можно сделать маршевую лестницу или, наоборот, очень компактную и элегантную винтовую лестницу – все будет зависеть от площади дома и высоты его перекрытий. Создать красивую конструкцию вам помогут многочисленные фото в интернете, но для того чтобы правильно ее спроектировать, вам придется вспомнить школьные годы и заняться математикой.
При расчете угла наклона лестницы нужно учитывать множество нюансов — о них вы узнаете из статьи
Содержание статьи
Какой угол наклона должен быть у лестницы?
Как правило, практически все лестницы имеют наклон в 45˚. Ширина ступеньки должна соответствовать 45-му размеру ноги, но не меньше 30 см, чтобы человек не упал, спускаясь вниз. Обратите внимание, если вы сделаете через чур широкие ступеньки, то вы собьетесь с шага, а при чрезмерном уменьшении ширины затрудните себе спуск.
В принципе, угол подъема не так уж и сложно вычислить, зная высоту потолков и длину подошвы лестницы. Существует несколько способов:
- Осуществить все необходимые замеры. Просто замеряйте рулеткой расстояния между соприкосновением потолка со стеной и местом расположения нижней ступеньки.
- Произвести специальный расчет. Представьте длину и высоту треугольника в качестве катетов прямоугольного треугольника, а длина лестничного полотна будет вычисленной гипотенузой.

На фотографии — вариант лестницы с вполне удобными углами наклона. Несмотря на то, лестница выглядит необычно, подниматься на второй этаж по ней не составляет сложностей
Максимальный угол наклона
Для того чтобы понять, какой максимальный угол может быть у лестницы, разобьем все имеющиеся их виды на группы с характерным им углом наклона:
- Бытовые лестницы, предназначенные для жилых помещений – угол наклона от 30˚ до 45˚;
- Пандусы, пологие лестницы – максимальный уклон равняется 30-ти градусам;
- Приставные, крутые лестницы – от 45˚ до 75˚;
- Эвакуационные, хозяйственные лестницы имеют угол наклона свыше 75˚.
А вот наклон менее 23˚ для лестницы внутреннего назначения даже не обсуждается, так как никто не будет тратить метры жилплощади на «укладку лежащей» лестницы. Даже сложно себе представить, какой длины она должна быть с таким маленьким уклоном для подъема на следующий этаж, при высоте потолков в 3 метра.
Важно! Не рекомендованный угол наклона могут использовать при возведении нестандартных лестниц, как правило, в зданиях с маленькой площадью.
Комфортный угол наклона
Самым комфортным углом наклона считается 40 – 45˚, однако такая конструкция является очень громоздкой, поэтому ее обычно используют в больших помещениях.
Лестница, имеющая угол наклона 30 – 36˚ довольно компактна, но не такая удобная. Подъем на такую лестничную конструкцию будет удобен, а вот спуск довольно опасен, поэтому его лучше производить спиной вперед.

Лестница, изображенная на фотографии, имеет наиболее комфортный угол наклона. Единственный её недостаток в том, что она занимает довольно много пространства в комнате.
Прежде чем приступать к возведению лестницы, нужно «просканировать» все пространство, имеющееся в вашем доме. Каждое помещение должно использоваться максимально, поэтому нужно произвести расчеты и выбрать вариант, при котором лестница не будет занимать много места.
Следует обязательно устанавливать перила, если ступенек в вашей конструкции больше трех. Ширина ступеней должна быть около 0,28 – 0,30 метров, а высота – 0,15 – 0,18 метров. Когда все ступеньки одинакового размера – это повышает безопасность ее использования.
Стандартный угол наклона
Как уже говорилось ранее, стандартным и наиболее оптимальным углом наклона лестничной конструкции считается 40 – 45˚. Но так как такая лестница очень большая и занимает много места, многие люди пренебрегают данными рекомендациями. Приведем вам советы экспертов по уклону марша и размерам ступеней.
Размер ступеней лестниц в миллиметрах и рекомендованный уклон лестничной конструкции:
| 400 | 100 | 14 ° 11 ’ |
| 380 | 110 | 16 ° 21 ’ |
| 360 | 120 | 18 ° 31′ |
| 340 | 130 | 21 ° 00 ’ |
| 320 | 140 | 23 ° 11 ’ |
| 300 | 150 | 26 ° 41 ’ |
| 280 | 160 | 29 ° 51 ’ |
| 260 | 170 | 33 ° 11 ’ |
| 240 | 180 | 37 ° 00 ’ |
| 220 | 190 | 40 ° 51 ’ |
| 200 | 200 | 45 ° 00 ‘ |
Идеальный угол наклона
Угол пролета, в большинстве случаев, составляет от 20˚ до 50˚. Наиболее идеальным считается уклон, который колеблется в пределах 30 – 45˚. Но, к сожалению, не у каждого человека есть много места для того чтобы разметить такую удобную лестничную конструкцию.
Обратите внимание, чем меньше значение угла, тем опаснее по ней будет передвигаться, и чем больше угол, тем громоздче она будет.
Важно! Комфортный шаг при подъеме по лестнице с наклоном больше 45-ти градусов практически невозможен, а вот совершать спуск по ней вы сможете без опаски только лишь спиной вперед. Наверное, не стоит, и говорить о детях, которым по такой лестнице взобраться не получится.
Как рассчитать угол наклона лестницы
Рассчитать угол наклона лестницы можно по одному показателю – длине шага при спокойной ходьбе по горизонтальной поверхности взрослым человеком. Уклон определенных маршей рассчитывается отдельно в зависимости от количеств и высоты ступеней. Если у вас есть готовый проект, то угол лестницы определяется неимоверно просто.

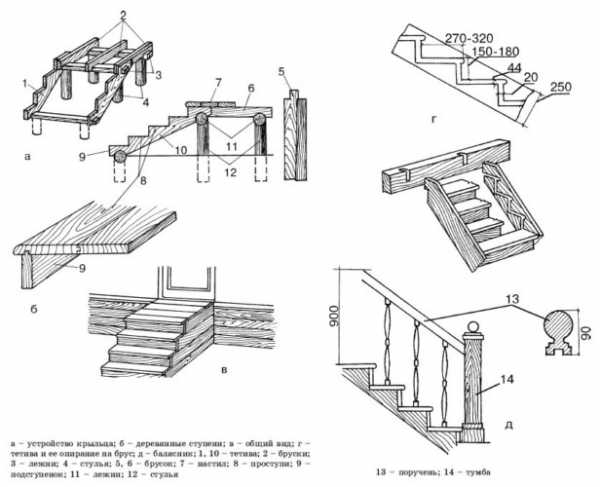
На схеме можно увидеть, какие углы наклона лестницы подходят для использования, а какие являются недопустимыми
Высота ступеней будет идеальной при значении 150 – 180 мм, ширина – 280 – 300 мм. Придерживаясь таких стандартов, угол наклона можно рассчитать по формуле: 2х + у = 580/660 мм, где х – это высота ступеней, а у – ширина. При размере ступеней меньше 145 мм, нужно использовать другую формулу: х + у.
В вышеприведенных формулах используют ширину, которая равняется среднему размеру стопы человека, и высоту, соответствующую размеру шага. Из этого можно сделать вывод, что чем ниже ступенька, тем шире она должна быть, и наоборот.
Угол наклона лестницы по ГОСТ
Думая о строительстве лестницы в своем доме, нужно помнить, что изготовляться они должны по ГОСТ и СНИП, основные положения которых говорят о :
- Если в доме более двух этажей, то лестницы должны иметь один пролет;
- Ширина конструкции, для прохождения одного человека, должна быть не меньше 80-ти см, а для прохождения 2-х людей – не менее 1-го метра;
- Марши должны иметь не менее 3-х и не более 18-ти ступеней;
- Уклон лестничной конструкции нужно делать не более 1:1 (угол подъема должен составлять 45°) и не менее 1:2 (угол подъема — 26° и 40′).При подъеме по уклону больше 50˚ используют лестницы приставного типа, для подъема по склону менее 5˚ – используют пандусы. Самыми удобными считаются лестничные конструкции, имеющие уклон 26°7’/30°.
Интересный факт! Количество ступенек в марше лучше делать нечетным, так как людям комфортней начинать и завершать подъем или спуск по лестнице одной и той же ногой.
Угол наклона приставной лестницы
Приставная лестничная конструкция упирается в пол и в стену тетивами так, чтобы полностью сохранять устойчивость и в тоже время предоставить возможность подняться к труднодоступному месту.
Угол наклона приставной лестничной конструкции составляет около 60 – 75˚, поэтому подъем и спуск по такой конструкции довольно затруднителен, а перенос каких-либо грузов – вообще невозможен.
Видео
Из видео вы узнаете, как правильно смонтировать лестницу на чердак, а также различные тонкости, которые необходимо учитывать при монтаже.
Ничего сложного в проектировании лестницы нет. Главное – это следуйте формулам и установленным правилам, правильно рассчитайте ширину и длину конструкции в общем, а также количество ступней и угол наклона. Грамотно сконструированная и добротно смонтированная лестница прослужит вам долгие годы.
| Уголки высоты / наклона и Углы подъема или наклона углов над горизонтом, как если бы вы смотрели с уровня земли в вершина флагштока.Углы депрессии или склонения - это углы ниже горизонтали, как если бы вы смотрели из окна вниз на основание здание на соседнем участке. Всякий раз, когда у вас есть один из этих углов, вы следует сразу начать представлять, как прямоугольный треугольник впишется в описание.
Две десятых мили составляют 0,2 × 5280 футов = 1056 футов, так что это мое горизонтальное расстояние. Мне нужно найти высоту х кактуса.Итак, я рисую прямоугольный треугольник и маркирую все, что знаю: .
До ближайшей ноги Сагуаро имеет высоту 44 футов.
Мне нужно выполнить это упражнение по шагам. Я не могу найти высоту башни, AB, пока у меня не будет длины базового компакт-диска.(Представьте, что D перемещается вправо, чтобы встретить продолжение AB, образуя прямоугольный треугольник.) Для этого вычисления я буду использовать высоту холма. Чтобы минимизировать ошибку округления, я буду использовать все цифры из моего калькулятора в моих вычислениях, и пытаюсь "унести" все вычисления в моем калькуляторе .. Теперь, когда у меня есть длина основания, Я могу найти общую высоту, используя угол, который измеряет высоту от уровня моря до вершины башни. Отлично! Сохраняя все цифры и проводя вычисления в своем калькуляторе, я получил точный ответ. Без округления! Но мне нужно вычесть, потому что "300" высота от воды до вершины башни. Первая сотня метров этой общей высоты - холм, итак: Вверх | Вернуться к индексу
|
| НАЙТИ УРОК Этот урок можно распечатать для личного пользования.
|
Как рассчитать стороны и углы треугольников
Тригонометрия и основы треугольников
В этом руководстве вы узнаете о тригонометрии, которая является разделом математики, который охватывает отношения между сторонами и углами треугольников. Сначала мы рассмотрим основные факты о треугольниках, а затем узнаем о теореме Пифагора, правиле синуса, правиле косинуса и о том, как их использовать для вычисления всех углов и длин сторон треугольников, когда вы знаете только некоторые из углов или сторон. длины.Вы также откроете для себя различные методы определения площади треугольника.
Поделитесь ссылкой на это руководство со своими друзьями в Pinterest, Facebook или других социальных сетях, если вы сочтете его полезным.
Что такое треугольник?
По определению, треугольник - это многоугольник с тремя сторонами.
Многоугольники - это плоские фигуры с несколькими прямыми сторонами. «Плоскость» просто означает, что они плоские и двухмерные. Другие примеры многоугольников включают квадраты, пятиугольники, шестиугольники и восьмиугольники.Слово «плоскость» происходит от греческого polús , означающего «много», и gōnía , что означает «угол» или «угол». Итак, многоугольник означает «много углов». Треугольник - это простейший многоугольник, имеющий только три стороны.
Основные сведения о треугольниках
Самым основным фактом о треугольниках является то, что в сумме все углы составляют 180 градусов. Угол между сторонами может быть от 0 до 180 градусов. Углы не могут быть 0 или 180 градусов, потому что треугольники станут прямыми линиями.(Они называются вырожденными треугольниками ).
Градусы можно записать с помощью символа º. Итак, 45º означает 45 градусов.
Треугольники бывают разных форм и размеров в зависимости от углов их углов. Некоторые треугольники, называемые подобными треугольниками, имеют одинаковые углы, но разную длину сторон. Это изменяет соотношение треугольника, делая его больше или меньше, без изменения степени его трех углов.
Ниже мы рассмотрим множество способов определения длин сторон и углов треугольника.
Что такое теорема о неравенстве треугольника?
Это означает, что сумма любых двух сторон треугольника должна быть больше или равна оставшейся стороне.
Какие существуют типы треугольников?
Прежде чем мы научимся определять стороны и углы треугольника, важно знать названия различных типов треугольников. Классификация треугольника зависит от двух факторов:
- Длина сторон треугольника
- Углы углов треугольника
Ниже приведены график и таблица, в которых перечислены различные типы треугольников, а также описаны их уникальные особенности.
Типы треугольников
Треугольник можно классифицировать по длине стороны или внутреннему углу.
Использование греческого алфавита для уравнений
Еще одна тема, которую мы кратко рассмотрим, прежде чем углубляться в математику решения треугольников, - это греческий алфавит.
В науке, математике и технике многие из 24 символов греческого алфавита заимствованы для использования в диаграммах и для описания определенных величин.
Вы, возможно, видели, что символ μ (мю) представляет микрограммы в микрограммах мкг или микрометрах-мкм.Заглавная буква Ω (омега) в электротехнике обозначает ом. И, конечно же, π (pi) - это отношение длины окружности к диаметру круга.
В тригонометрии символы θ (тета) и φ (фи) часто используются для обозначения углов.
Как найти стороны и углы треугольника?
Существует множество методов определения сторон и углов треугольника. Чтобы найти длину или угол треугольника, можно использовать формулы, математические правила или знание того, что углы всех треугольников в сумме составляют 180 градусов.
Инструменты для определения сторон и углов треугольника
- Теорема Пифагора
- Правило синуса
- Правило косинуса
- Тот факт, что все углы в сумме дают 180 градусов
Теорема Пифагора (Теорема Пифагора)
Теорема Пифагора использует тригонометрию для определения самой длинной стороны (гипотенузы) прямоугольного треугольника (прямоугольный треугольник в британском английском). В нем указано, что для прямоугольного треугольника:
Квадрат на гипотенузе равен сумме квадратов на двух других сторонах.
Если стороны треугольника - это a, b и c, а c - гипотенуза, теорема Пифагора утверждает, что:
c² = a² + b²
c = √ ( a² + b²)
Гипотенуза - это самая длинная сторона прямоугольного треугольника, расположенная напротив прямого угла.
Итак, если вы знаете длины двух сторон, все, что вам нужно сделать, это возвести эти две длины в квадрат, сложить результат, а затем извлечь квадратный корень из суммы, чтобы получить длину гипотенузы.
Пример задачи с использованием теоремы Пифагора
Стороны треугольника имеют длину 3 и 4 единицы. Какова длина гипотенузы?
Назовите стороны a, b и c. Сторона c - гипотенуза.
a = 3
b = 4c = Неизвестно
Итак, согласно теореме Пифагора:
c² = a² + b²
Итак, c² = 3² + 4² = 9 + 16 = 25
с = √25
с = 5
Как вы измеряете углы?
Можно использовать транспортир или цифровой угловой искатель.Они полезны для поделок и строительства, если вам нужно измерить угол между двумя сторонами или перенести угол на другой объект. Вы можете использовать его как замену конусу для переноса углов, например. при разметке концов стропил перед обрезкой. Линейки градуированы в дюймах и сантиметрах, а углы могут измеряться с точностью до 0,1 градуса.
Обратите внимание, что это не подходит в качестве инструмента для технического рисования, потому что ступица не будет лежать на бумаге, в отличие от транспортира.Кроме того, поскольку он изготовлен из нержавеющей стали, у него есть острые углы, которые могут быть острыми и поэтому не подходят для маленьких детей.
Синус, косинус и тангенс угла наклона
Прямой треугольник имеет угол 90 градусов. Сторона, противоположная этому углу, известна как гипотенуза (другое название самой длинной стороны). Длину гипотенузы можно определить с помощью теоремы Пифагора, но для определения двух других сторон необходимо использовать синус и косинус. Это тригонометрические функции угла.
На схеме ниже один из углов обозначен греческой буквой θ. Сторона a известна как «противоположная» сторона, а сторона b «примыкает» к углу θ.
Вертикальные линии «||» слова внизу означают «длина».
синус θ = | противоположная сторона | / | гипотенуза |
косинус θ = | смежная сторона | / | гипотенуза |
Желто-коричневый θ = | противоположная сторона | / | прилегающая сторона |
Синус и косинус применяются к углу, любому углу, поэтому можно иметь две линии, пересекающиеся в точке, и оценивать синус или косинус для этого угла.Однако синус и косинус получаются из сторон воображаемого прямоугольного треугольника, наложенного на линии.
Например, на второй диаграмме выше фиолетовый треугольник разносторонний, а не прямоугольный. Однако вы можете представить прямоугольный треугольник, наложенный на фиолетовый треугольник, из которого можно определить противоположную, смежную и гипотенузу стороны.
В диапазоне от 0 до 90 градусов синус находится в диапазоне от 0 до 1, а cos находится в диапазоне от 1 до 0.
Помните, синус и косинус зависят только от угла, а не от размера треугольника.Таким образом, если длина a изменяется на диаграмме выше, когда треугольник изменяется в размере, гипотенуза c также изменяется в размере, но отношение a к c остается постоянным. Они похожи на треугольники.
Синус и косинус иногда сокращаются до sin и cos.
Правило синуса
Отношение длины стороны треугольника к синусу противоположного угла постоянно для всех трех сторон и углов.
Итак, на схеме ниже:
a / синус A = b / синус B = c / синус C
Теперь вы можете проверить синус угла с помощью научного калькулятора или найти его в Интернете.Раньше, до появления научных калькуляторов, нам приходилось искать значение синуса или cos угла в книге таблиц.
Противоположная или обратная функция синуса - это арксинус или «обратный синус», иногда записываемый как sin -1 . Когда вы проверяете арксинус значения, вы вычисляете угол, который произвел это значение, когда с ним применялась функция синуса. Итак:
sin (30º) = 0,5 и sin -1 (0,5) = 30º
Правило синуса следует использовать, если...
Длина одной стороны и величина противоположного угла известны. Затем, если известны какие-либо другие оставшиеся углы или стороны, можно вычислить все углы и стороны.
Правило косинуса
Для треугольника со сторонами a, b и c, если a и b известны и C - это включенный угол (угол между сторонами), C можно вычислить с помощью правила косинуса. Формула выглядит следующим образом:
c 2 = a 2 + b 2 - 2ab cos C
Правило косинуса следует использовать, если...
- Вам известны длины двух сторон треугольника и прилегающий угол. Затем вы можете определить длину оставшейся стороны, используя правило косинуса.
- Вы знаете длину всех сторон, но ни одного угла.
Затем, переставив уравнение правила косинусов:
C = arccos ((a 2 + b 2 - c 2 ) / 2ab)
Остальные углы обрабатываются аналогично.
Как найти углы треугольника, зная соотношение длин сторон
Если вы знаете соотношение длин сторон, вы можете использовать правило косинуса для вычисления двух углов, тогда оставшийся угол можно найти, зная, что все углы складываются. до 180 градусов.
Пример:
У треугольника соотношение сторон 5: 7: 8. Найдите углы.
Ответ:
Итак, назовите стороны a, b и c и углы A, B и C и предположите, что стороны равны a = 5 единиц, b = 7 единиц и c = 8 единиц.Не имеет значения, какова фактическая длина сторон, потому что все похожие треугольники имеют одинаковые углы. Итак, если мы вычислим значения углов для треугольника со стороной a = 5 единиц, это даст нам результат для всех этих похожих треугольников.
Используйте правило косинуса. Итак, c² = a² + b² - 2ab cos C
Заменяет a, b и c, давая:
8² = 5² + 7² - 2 (5) (7) cos C
Вычисление дает:
64 = 25 + 49 - 70 cos C
Упрощение и перестановка:
cos C = 1/7 и C = arccos (1/7).
Вы можете снова использовать правило косинуса, чтобы найти второй угол, и третий угол можно найти, зная, что все углы складываются в 180 градусов.
Как определить площадь треугольника
Есть три метода, которые можно использовать для определения площади треугольника.
Метод 1. Использование высоты перпендикуляра
Площадь треугольника можно определить, умножив половину длины его основания на высоту перпендикуляра. Перпендикулярно означает под прямым углом.Но с какой стороны база? Что ж, вы можете использовать любую из трех сторон. Используя карандаш, вы можете проработать область, проведя перпендикулярную линию от одной стороны к противоположному углу, используя заданный квадрат, Т-образный квадрат или транспортир (или плотницкий квадрат, если вы что-то строите). Затем измерьте длину линии и используйте следующую формулу, чтобы получить площадь:
Площадь = 1 / 2ач
«a» представляет длину основания треугольника, а «h» представляет высоту перпендикулярной линии.
Метод 2. Использование длин сторон и углов
Приведенный выше простой метод требует, чтобы вы действительно измерили высоту треугольника. Если вы знаете длину двух сторон и включенный угол, вы можете вычислить площадь аналитически, используя синус и косинус (см. Диаграмму ниже).
Метод 3. Воспользуйтесь формулой Герона
Все, что вам нужно знать, - это длины трех сторон.
Площадь = √ (s (s - a) (s - b) (s - c))
Где s - полупериметр треугольника
.s = (a + b + c) / 2
Угол наклона прямой - Concept
Угол наклона прямой - это угол, образованный пересечением прямой и оси x. Использование горизонтального «пробега» 1 и m для наклона, угла наклона, theta = tan-1 (м) или m = tan (theta). Следовательно, если угол или наклон известен, другой можно найти с помощью одного из уравнений. Если угол наклона отрицательный, то и наклон линии отрицательный.
Какой угол наклона лески? Итак, у меня есть линия, нарисованная здесь уравнением y = mx + b, оно должно быть вам знакомо. Это угол наклона тета, это угол между линией и горизонталью. Теперь я хочу выяснить, как я могу вычислить эту линию, как она соотносится с уравнением линии, поэтому я нарисовал здесь маленький треугольник, а затем я обозначу стороны, скажем, я обозначу это 1, что будет с этой стороны быть? Теперь я знаю, что наклон, наклон линии равен подъему над пробегом, поэтому наклон будет равен вопросительному знаку над 1, так что это будет наклон.
Теперь, если я посмотрю на этот прямоугольный треугольник, и это прямоугольный треугольник, я могу использовать тригонометрию прямоугольного треугольника, чтобы найти взаимосвязь между тета и m, верно? m - это длина по вертикали этой стороны, поэтому тангенс теты равен m по касательной к 1, тета равен m, поэтому это соотношение между углом наклона и наклоном, тангенс угла наклона - это наклон, а угол наклона равен арктангенс угла наклона, поэтому вы можете рассчитать наклон по углу наклона, а угол наклона можно рассчитать по углу наклона.
Теперь давайте посмотрим на другой, на несколько частных случаев. Горизонтальные или вертикальные линии. Теперь горизонтальная линия не обязательно будет пересекать ось x, конечно, для линии до y = 0 это ось x, но мы определяем ее угол наклона равным 0, и, конечно же, тангенс 0 равен 0, поэтому наклон будет касательной к 0, который равен 0, и это то, что мы, как мы определяем наклон горизонтальной линии, это 0.
А как насчет вертикальной? Что ж, я бы сказал, что здесь угол наклона пи больше 2, поэтому тета больше пи больше 2, каков наклон? Касательная к тэте, прямая касательная к пи более 2, но, конечно, это не определено, и это именно то, что мы хотели бы, чтобы наклон вертикальной линии не был определен, нет наклона, поэтому просто для просмотра, угол наклона линии угол, на который Линия определяет отношение к горизонтали, а наклон - это тангенс теты, угол наклона равен наклону, а угол наклона равен обратному тангенсу наклона.
ios - Расчет угла поворота вместо наклона для углов более 360 градусов
Переполнение стека- Около
- Товары
- Для команд
- Переполнение стека Общественные вопросы и ответы
- Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
- Вакансии Программирование и связанные с ним технические возможности карьерного роста